5366. Крестный отец
В прошлом году в
Чикаго произошло большое количество гангстерских нападений и странных убийств.
Начальник полиции устал от всех этих преступлений и решил арестовать лидеров
мафии.
К несчастью,
структура мафии в Чикаго достаточно сложная. Известно, что мафия состоит из n человек. Полиция наблюдала некоторое
время за ними и установила, кто с кем общается. Основываясь на этих данных, шеф
полиции обнаружил, что иерархия мафии может быть представлена в виде дерева.
Глава мафии, крестный отец, находится в корне дерева. Если члена мафии
представить в виде вершины дерева, то его непосредственные подчиненные являются
детьми этой вершины. По правилам конспирации гангстеры общаются только со
своими непосредственными подчиненными и начальниками.
Несмотря на
имеющуюся сеть коммуникаций, полиция не знает, кто в каждой паре общающихся
людей является начальником, а кто подчиненным. То есть известно только
неориентированное дерево коммуникаций, в котором неизвестно кто является
крестным отцом.
Крестный отец
хочет иметь наибольший контроль над остальными членами мафии. Основываясь на
этой информации, шеф полиции сделал предположение, что крестным отцом является
тот, после удаления кого из коммуникационного дерева, размер наибольшей из
образовавшихся связных компонент будет наименьшим. Помогите полиции найти
потенциальных крестных отцов и арестовать их.
Вход. Первое число содержит количество людей n, входящих в мафию (2 ≤ n ≤ 50000). Все члены мафии
пронумерованы числами от 1 до n.
Далее следует n – 1 пара чисел ai, bi, означающих, что гангстер ai общается с гангстером bi. Гарантируется, что сеть общения гангстеров образует
дерево.
Выход. В одной строке в возрастающем порядке
вывести номера всех бандитов, которые могут быть крестными отцами. Выводимые
числа разделять одним пробелом.
|
Пример
входа 1 |
Пример
выхода 1 |
|
6 1 2 2 3 2 5 3 4 3 6 |
2 3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 1 4 3 4 2
4 5 4 |
4 |
РЕШЕНИЕ
графы -
поиск в глубину
Анализ алгоритма
Пусть имеется дерево из n вершин.
Центроидом дерева называется такая вершина, при удалении которой дерево
распадается на компоненты связности, количество вершин в
каждой из которых не более n / 2.
В задаче следует найти все центроиды дерева.
Рассмотрим примеры деревьев и их центроиды (отмечены зеленым
цветом).
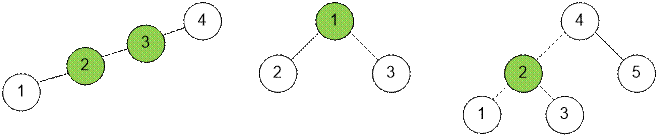
Запустим поиск в глубину dfs(v), который в sub[v] вычислит количество
бандитов в поддереве с вершиной v. Для приведенных
примеров возле каждой вершины v укажем
соответствующее ей значение sub[v] (поиск в глубину стартуем во всех примерах из вершины 1).
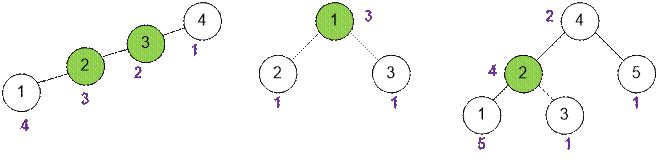
Если вершина v имеет сыновей to1,
to2, …, tok , то
sub[v] = 1 + sub[to1] + sub[to2] + … + sub[tok]
Вершина v является центроидом дерева тогда и только тогда, когда:
·
для каждого ее сына to имеет
место sub[to]
≤ n / 2;
·
если
из дерева удалить поддерево с корнем v,
то оно будет содержать не более n / 2 вершин: n – sub[v] ≤ n / 2;
Например, в правом на рисунке дереве с n = 5 вершинами центроидом будет
вершина 2, потому что
·
sub[4] = 2 ≤ n / 2;
·
sub[3] = 1 ≤ n / 2;
·
n – sub[2] = 5 – 4 =
1 ≤ n / 2;
Анализ алгоритма – 2
Удаление вершины дерева может разбить его не только на две,
но и на несколько компонент связности. Из первой вершины запустим функцию
поиска в глубину dfs(1). При этом dfs(k)
будет возвращать значение, на единицу большее количества бандитов, которые
являются для k - го подчиненными (не
только непосредственно). Единица добавляется, так как в dfs(k) учитывается также и k - ый бандит.
Как только для некоторого бандита i возвращаемое значение dfs(i)
превысит n / 2, то именно его можно
считать крестным отцом. В этом случае число бандитов, отнесенных к компоненте
связности, не содержащей 1, будет не более n
/ 2.
Если для некоторого бандита k значение 2 * dfs(k)
равно n, то число бандитов,
отнесенных к компоненте связности, содержащей 1, будет не более n / 2. В этом случае k - го бандита можно считать крестным
отцом. Если ни для какого k не
выполняется равенство 2 * dfs(k) = n, то крестным отцом может быть только
один бандит, найденный в предыдущем абзаце.
Пример
На рисунке
изображено дерево, приведенное в примере. Бандиты, которые могут быть
крестными отцами, отображены зеленым цветом. Корень дерева находится в вершине 1.
Возле каждой вершины v число обозначает
количество вершин в поддереве с корнем v (включая и сам
корень).
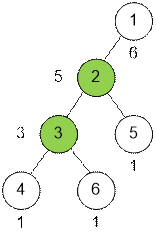
Значения
переменной res, возвращаемой вызовом
dfs(v), приведены в таблице:

Количество
вершин n в дереве равно 6.
Ровно половина
вершин будет отнесена к компоненте, содержащей вершину 1, если удалить вершину
с номером 3 (dfs(3) = 3, а значит с вершиной 1 останется 6 – 3 = 3 вершины).
Не больше
половины вершин будет отнесено к компоненте, не содержащей вершину 1 (если
таких компонент несколько, то можно рассматривать любую из них), если удалить
вершину с номером, для которой выполняются следующие условия:
1. возвращаемое
значение функции dfs будет строго больше n
/ 2 = 6 / 2 = 3.
2. возвращаемое
значение функции dfs будет наименьшим.
Таковой является
вершина 2, dfs(2) = 5.
Реализация алгоритма
Информацию о
графе будем хранить в списке смежности g.
vector<vector<int> > g;
Функция dfs возвращает количество бандитов в
поддереве с вершиной v и сохраняет это
значение в sub[v].
int dfs(int v, int p = -1)
{
sub[v] = 1;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (to != p) sub[v] += dfs(to, v);
}
return sub[v];
}
Функция centroid совершает поиск в глубину, находит и заносит центроиды в
массив centr.
void centroid(int v, int p = -1)
{
Установим flag =
1, если вершина v является центроидом.
int flag = 1;
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v][i];
if (to == p) continue;
Если для сына to выполняется sub[to] > n / 2, то v не является центроидом.
if (sub[to] > n / 2) flag = 0;
Если для сына to выполняется sub[to] < n / 2, то в поддереве с корнем to не содержится центроидов. Есть смысл продолжать поиск в сыне
to, если только sub[to] ≥ n / 2.
if (sub[to] >= n / 2) centroid(to, v);
}
Дерево без поддерева с корнем v содержит n – sub[v] вершин.
Если оно содержит более n / 2 вершин, то v не центроид.
if (n - sub[v] > n / 2) flag = 0;
Если
для вершины v выполняются все
условия центроида, то заносим ее в массив centr.
if (flag) centr.push_back(v);
}
Основная часть программы.
Инициализируем массивы.
scanf("%d",&n);
g.resize(n+1);
sub.resize(n+1);
Читаем входной граф.
for(i = 0; i < n - 1; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
}
Запускаем поиск в глубину, ищем
центроиды дерева – крестных отцов.
dfs(1);
centroid(1);
Сортируем центроиды.
sort(centr.begin(),
centr.end());
Выводим крестных отцов в возрастающем
порядке.
for (i = 0; i < centr.size(); i++)
printf("%d ", centr[i]);
printf("\n");
Реализация алгоритма – 2
Информацию о
графе будем хранить в списке смежности g.
vector<vector<int> > g;
Функция dfs возвращает значение, на единицу
большее количества бандитов, являющихся для v - го
подчиненными. В переменной p хранится предок вершины v.
int dfs(int
v, int p = -1)
{
int i, res =
1;
for(i = 0; i
< g[v].size(); i++)
{
int to =
g[v][i];
if (to ==
p) continue;
res += dfs(to,v);
}
if ((ans ==
0) && (res >= n / 2 + 1)) ans = v;
if (res * 2
== n) ans1 = v;
return res;
}
Основная часть программы.
Инициализируем массивы.
scanf("%d",&n);
g.resize(n+1);
Читаем входной граф.
for(i = 0; i < n - 1; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
}
Запускаем поиск в глубину, ищем
крестных отцов.
ans1 = ans = 0;
dfs(1);
Выводим крестных отцов в возрастающем
порядке.
if (ans1) printf("%d %d\n",min(ans, ans1),max(ans, ans1));
else printf("%d\n",ans);